4.5.lPID控制器原理

  PID控制器是一种线性控制器,它根据给定值r(t)和实际输出值y(t)构成控制偏差e（t）

  再按比例、积分、微分运算后构成PID控制规律

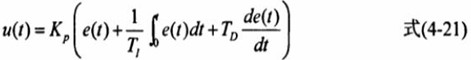
  写成传递函数的形式为：

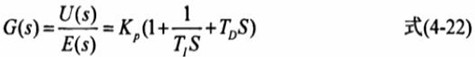
  式中K_p为比例系数,T₁为积分时间常数,T_D为微分时间常数,原理如图4.13所示：

下面简单介绍比例部分、积分部分和微分部分的作用。

1.比例调节器(P)

  它的输出和偏差信号成正比,只要偏差出现,就能及时地产生与之成比例的调节作用。调节的强弱取决于比例系数Kn的大小,K,越大系统的响应速度越快, 系统的调节精度越高,但是容易产生超调,系统的稳定性变差。如果K取值过小, 系统响应速度变慢,调节时间加长,稳定性变坏。

2.比例积分调节器PI)

  只要石英晶振系统存在误差,积分控制作用就不断积累,输出控制量以消除误差,因而只要有足够的时间,积分将能完全消除误差。参数T的一个最主要作用就是消除系统的稳态误差,T越大系统稳态误差消除的越快,但也不能过大,否则在响应过程的初期产生积分饱和现象,若T过小,系统的稳态误差难以消除,影响系统的调节精度。

3.比例微分调节器(PD)

  微分控制可以减小超调量,克服振荡,使石英晶体振荡器系统的稳定性提高,同时加快系统的动态响应速度,减小过渡过程时间,从而改善系统的动态性能,具有“前导” 作用,但T不能过大,否则会使响应过程提前制动,延长调节时间,并且会降低系统的抗干扰能力。

  为了能在数字信号处理器中实现对系统的PD控制,必须对其进行离散化处理。常见的数字PID控制方法有位置式和增量式,位置式PID算法每次输出与整个过去状态有关,计算式中要用到过去偏差的累加值,容易产生较大的累积误差;而增量式PID只需计算增量,当存在计算误差或精度不足时,对控制量计算的影响较小。因为这里PD控制器的执行单元是DA转换器,其转换输出的电压用来调节OCXO晶振的频率,因此需要的是控制的绝对数值,而不是控制的增量,所以位置式PID控制算法在这里比较合适,下面将简单介绍位置式PD控制算法。

  当采样时间T很短时,采用数字逼近的方法,利用求和代替积分:

  式中,T为采样周期;k为采样序号;e(k)为系统在第k次采样时刻的偏差值; e(k-1)为系统在第(k-1)次采样时刻的偏差值。

离散PID表达式；

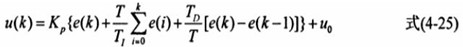
  一般称K为比例系数,K₁=K_P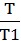为积分系数, K_D=K_P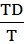为微分系数,依次称为比例项、积分项和微分项。

  由式(425)可得第(k-1)次样时刻的控制量为:

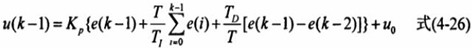
用式(4-25减去式(K-1)可得:

  这就是位置式PID的递推公式,在进行数字化离散后编程用的就是这个公式。