

CEOB2B晶振平台接着讲述《如何确定石英晶体各级温度系数(一)》的下半部分内容。
下表给出了各级频率温度系数的数值,以及这些系数随切角的变化率,将表中有关数据代入下式,即可作出所需的频率温度特性曲线。
表3.2.1AT切各级频率温度系数的及其随切角的变化

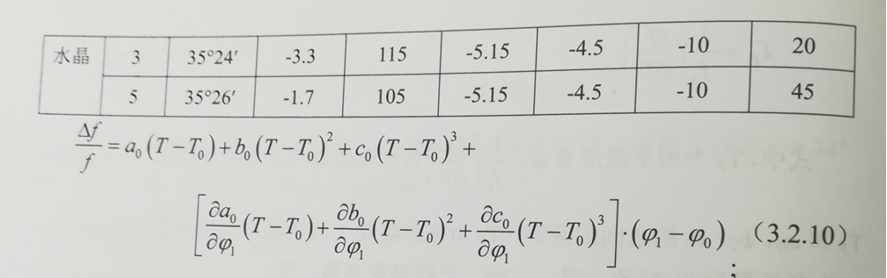

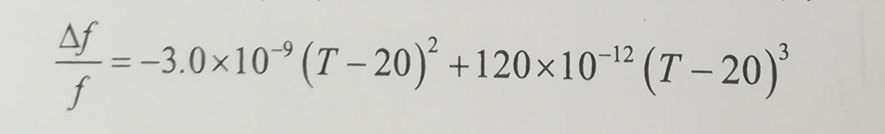
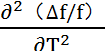

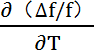

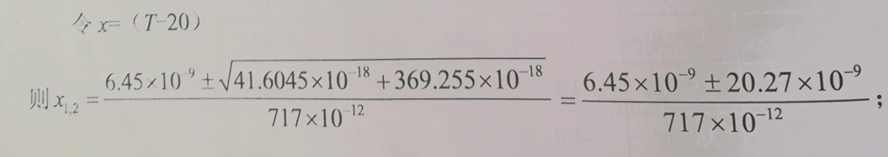




则(T-Ti)=-0.078/0.0657=-1.19℃,当Ti=27℃时,则T=27-1.19=25.89℃,即为拐点温度。
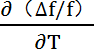


上述所计算的结果与实际生产的石英晶体元件的测量结果比较接近。
CEOB2B晶振平台是全球领先的晶振单一采购平台,平台里汇集了数千万中晶振产品,石英晶振,贴片晶振,有源晶振,温补晶振,差分晶振等,只要您需要的,这里统统给您准备好了,并每天更新技术资料解决产品方案.